بِسْم الله الرحمن الرحيم،
في المقال السابق عرَّفنا بشبكات التفاعل الحيوي و أهمية دراستها . في هذا المقال سوف نكمل الحديث عن شبكات التفاعل الحيوي لكن من الجانب العملي، حيث سوف نحاول ان نعطي لمحة عن كيفية التعامل مع شبكات التفاعل الحيوي برمجيا باستعمال لغة R و نُعَرف ببعض الأدوات التي يمكن استعمالها من طرف المبرمجين. لكن قبل الخوض في البرمجة سوف نقوم اولا بتعريف الشبكات تعريفا رياضيا من وجهة نظر نظرية المخططات (Graph theory).
التعريف الرياضي للشبكات
تُعَرف الشبكة (المخطط او البيان)  رياضيا على انها زوح مرتب
رياضيا على انها زوح مرتب  حيث تمثل
حيث تمثل  مجموعة العقد (nodes) في المخطط و تمثل
مجموعة العقد (nodes) في المخطط و تمثل  مجموعة الأضلاع (edges) . تصنف الشبكات على حسب نوع اضلاعها الى نوعين:
مجموعة الأضلاع (edges) . تصنف الشبكات على حسب نوع اضلاعها الى نوعين:
- الشبكات الغير موجهة: لايهم اتجاه الاضلاع فيها, مثلا في شبكات التفاعل بين البروتينات.
- الشبكات الموجهة: وفيها تكون الاضلاع. يسمي الضلع الاول المصدر والثاني الهدف. مثلا في شبكات التنظيم الجيني تمثل الاتجاهات الجين المؤَثر والجين المتأثر.
- الشبكات الموزونة: وهي شبكات تكون أضلاعها ذات اهمية متفاوتة, لهذا يعطى لكل ضلع وزن يتناسب مع اهميته. يمكن لهذه الشبكات ان تكون موجهة او غير موجهة.
- الشبكات الغير الموزونة: وهي شبكات ذات اضلاع متساوية الاهمية.
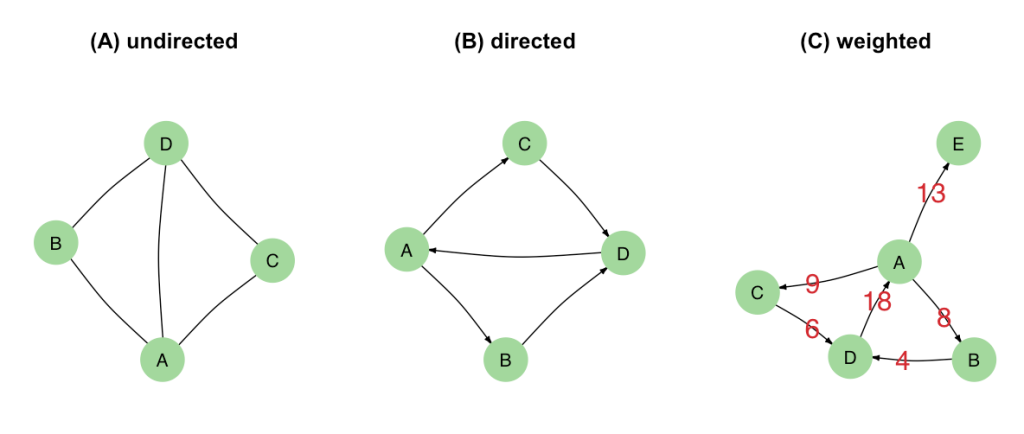
رسم بياني يبين انواع المخططات
تَعرف نظرية المخططات رواجا واسعا في عدة مجالات , خاصة في مجال تحليل الشبكات الرقمية و الشبكات الاجتماعية. في هذا المقال سوف نهتم باستعمالها في مجال الشبكات الحيوية لكن يكن استعمال كل هذه المفاهيم في العديد من المجالات مع الاختلاف في تفسير النتاءج.
يسمى المجال الذي يهتم بدمج الشبكات و المعلومات البيولجية بمجال الـ System biology. الكثير من العاملين في هذا المجال هم باحثين ذو خلفيات في الاعلام الآلي والعلوم الرياضية. لكن مع تزايد اهتمام البيولوجين والاطباء ادى الى تطوير خورزميات اكثر مناسبة للمشاكل البيولوجية
في العادة نهتم ببعض الخصائص الطبولوجية للمخطط حيث تساعدنا في فهم التكوين الداخلي للشبكة و معرفة العلاقة التي تربط الرؤوس ( في حالتنا الرؤوس هي المكونات الحيوية) . يساعدنا حساب بعض المعايير في دراسة خصائص الشبكة كتوزيع درجة العقد, قطرالشبكة, اهم العناصر في الشبكة, اقصر طريق,....الخ. في الفقرة القادمة سوف نعرف ببعض المعايير.
بعض المعايير المستعملة لدراسة خصائص الشبكات
من اهم المعايير المستعملة في دراسة خصائص الشبكات هي المعايير المركزية. يمكن تعريف المعايير المركزية على انها دوال  تعطي لكل راس
تعطي لكل راس  قيمة
قيمة  . تسمح لنا هذه القيمة بترتيب الرووس على حسب اهميتها. نقول ان العنصر
. تسمح لنا هذه القيمة بترتيب الرووس على حسب اهميتها. نقول ان العنصر  اهم من العنصر
اهم من العنصر  اذا كانت
اذا كانت  . في هذه الفقرة سوف نقوم بالتعريف ببعض المعاير المركزية الاكثر استعمالا في تحليل الشبكات البيولوجية.
. في هذه الفقرة سوف نقوم بالتعريف ببعض المعاير المركزية الاكثر استعمالا في تحليل الشبكات البيولوجية.
المركزيات المتعلقة بالرؤوس
1) مركزية درجة العُقَد (Degree centrality): وهي من المعايير البديهية في ترتيب الرؤوس, حيث تزداد اهمية الرأس (العقدة) مع زيادة درجتها. بالنسبة للشبكات الموجهة يتم حساب الـ in-degree وهو عدد الأضلاع المتجهة نحو الرأس و الـ out-degree وهو عدد الأضلاع الخارجة من الرأس ويساوي مجموعهما درجة الرأس (او العقدة). تعتبر مركزية درجة العقد كمعيار موضعي (او خاص بالراس) حيث تعطي معلومة عن عدد الاتصالات المباشرة بين الرأس والرؤوس المجاورة. مثلا في الشبكات البروتينية هذه المركزية تتناسب طردا مع البروتينات الأساسية. لكن المشكلة في مركزية درجة العقد انها متحيزة نحو العناصر المتصلة بكثرة. مثلا في الشبكات البروتينية هناك بروتينات تتركز عليها الدراسة بكثرة كبروتين P53 (الذي يؤدي توقفه الى حدوث العديد من السرطانات) وغيره من البروتينات المشهورة, وبالتالي في الشبكات البروتينية تكون هذه البروتينات مرتبطة بكثرة لتوفر معلومات اكثر عن البروتينات التي تتفاعل معها. اما البروتينات الغير مشهورة فتكون قليلة الارتباط ليس لانها غير مهمة لكن لاننا نجهل العديد من البروتينات التي تتفاعل معها.
2) مركزية القُرْبْ (Closeness centrality): يستعمل هذا المعيار لمعرفة الرؤوس التي تتمركز في مناطق كثيفة من الشبكة, حيث يتم حساب المسافة بين الرأس وكل الرؤوس الاخرى. رياضيا يتم حساب مركزية القرب للعنصر  كمقلوب مجموع المسافات نحو العناصر الاخرى:
كمقلوب مجموع المسافات نحو العناصر الاخرى:

في العادة تستعمل هذه المركزية في الشبكات الكثيفة. في مجال المعلوماتية الحيوية يمكن استعمال هذه المركزية لتحدير مراكز تسهيل التفاعل في شبكات التفاعل الايضي.
3) مركزية الوسطية (Betweenness centrality): تسعمل هذه الوسطية لتحديد الرؤوس التي يمكنها التحكم في الاتصلات داخل الشبكة, حيث تزداد اهمية العنصر كلما زادت قدرته على مراقبة الاتصالات. تحسب المركزية الوسطية لرأس من الرؤوس  كالتالي:
كالتالي:

حيث تمثل  عدد المسارات بين الرئسين
عدد المسارات بين الرئسين  و
و  التي تمر عبر
التي تمر عبر  . بالاضافة الى المعايير الاخرى, استُعملت المركزية الوسطية في العديد من الدراسات. مثلا من اجل دراسة البروتينات الرئيسية في شبكات التفاعل البروتيني (خاصة البروتينات ذات مركزية وسطية عالية و درجة ضعيفة) حيت تعتبر انها مهمة للدعم البنيوي للشبكة.
. بالاضافة الى المعايير الاخرى, استُعملت المركزية الوسطية في العديد من الدراسات. مثلا من اجل دراسة البروتينات الرئيسية في شبكات التفاعل البروتيني (خاصة البروتينات ذات مركزية وسطية عالية و درجة ضعيفة) حيت تعتبر انها مهمة للدعم البنيوي للشبكة.
المركزيات المتعلقة بالأضلاع
في بعض الاحيان نكون مهتمين بالأضلاع اكثر من الرؤوس, مثلا لمعرفة ماهي الاتصالات الاكثر اهمية في الشبكة او ماهو التفاعل الاكثر اهمية في الشبكة البولوجية. تقريبا تُعَرف مركزيات الاضلاع بطريقة مشابهة لمركزيات الرؤوس. من ابسط طرق ترتيب الاضلاع هي اعطائها اوزان مختلفة, مثلا بحساب المسافة بينها او نسبة التشابه او نسبة الارتباط (correlation) بينها. بالاضافة الى ذلك يمكننا ايضا حساب المركزية الوسطية للاضلاع باستعمال نفس تعريف المركزية الوسطيه للرؤوس.
بالإضافة الى هذه المركزيات (للرؤوس والأضلاع) هناك العديد من المركزيات الأخرى يمكن الاطلاع عليها في المراجع المقترحة.
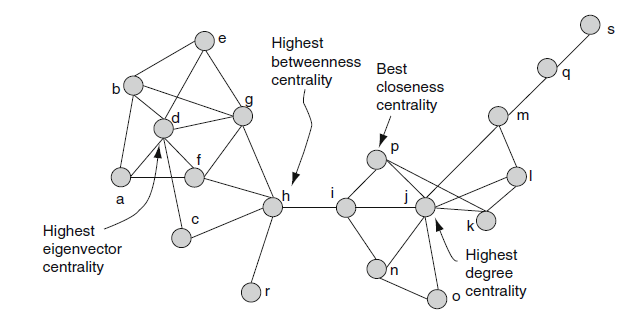
رسم بياني يوضح بعض انواع المركزيات
التعامل مع الشبكات الحيوية بلغة الآر
في لغة الآر كما في الغات الاخرى تم تطوير العديد من الحزم التي تتعامل مع الشبكات. برمجيا تمثل الشبكات على شكل مصفوفات كما هو مبين في البيان. حيث تمثل القيمة في المصفوفة وزن الضلع الرابط بين عنصرين. تسمى هذه المصفوفة بـ "مصفوفة المحاذات" (Adjacency Matrix).
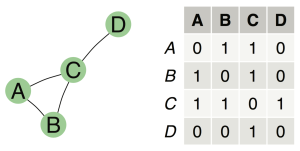
رسم بياني يوضح مفهوم مصفوفة المحاذات
هناك عدة حزم للتعامل مع الشبكات في لغة الآر, لكن من أشهرها حزمة igraph . تحتوي حزمة igraph على العديد من الدوال لانشاء الشبكات, اظافة خصائص لها, حساب بعض الخصائص, ايجاد المجوعات المترابطة و رسم الشبكات.
إنشاء الشبكات باستعمال igraph
يحتوي igraphعلى العديد من الدوال لانشاء الشبكات. يمكن تصنيف هذه الدوال الى ثلاثة انواع:
- دوال انشاء الشبكات من الملفات: مثل ملفات GML, pajek او ncol وغيرها من ملفات حفظ الشبكات.
- دوال انشاء الشبكات باستعمال مصفوفة المحاذات: حيث يمكن اعطائه مباشرة المصفوفة ويقوم بانشاء الشبكة (المخطط).
- دوال انشاء الشبكات باستعمال عبارات مخصصة: توفر
igraphلغة مبسطة لانشاء شبكات صغيرة من اجل القيام ببعض الإختبارات.
في العادة لما نتعامل مع الشبكات البيولوجية نقوم باستعمال شبكات كبيرة تكون محفوظة على شكل ملفات. من بين الصيع المستعملة هي ncol والتي تعطي معلومات عن كل ضلع في الشبكة. يُمَثل كل ضلع بثلاث معلومات: الرأس الأول, الرأس الثاني و وزن الضلع. اذا لم يحدد وزن الاضلاع فسيعتبرها igraph ان الاوزان مساوية لـ 1.
الصيغ الاخرى مثل GML مثلا هي على شكل ملفات xml وتحتوي على معلومات اكثر (مثلا الالوان و بعض خصائص كل رأس وضلع).
في igraphنقوم بقراءة هذه الملفات باستعمال دالة read.graphمع تحديد نوع الملف الذي نريد قراءته. مثلا ليكن لدينا الشبكة البروتينية التالية المحفوظة في الملف test_graph.ncol :
CRHR2 UCN CRHR2 CRH CRHR2 UCN2 CRHR2 UCN3 UCN CRHBP UCN CRHR1 CRH CRHR1 UCN2 IL10RB UCN3 CRHR1 UCN3 IL10RB IL10RB IL22 IL10RB IL28A IL10RB IL10 IL10RB IL10RA IL10RB IL28B IL22RA2 IL22 IL22 IL22RA1 IL28RA IL28A IL28RA IL29 IL10 IL10RA
نقوم بقراءة الملف كالتالي:
library(igraph)
G <- read.graph("test_graph.ncol",format="ncol")
G
# IGRAPH UN-- 17 20 --
# + attr: name (v/c)
# + edges (vertex names):
# [1] CRHR2 --UCN CRHR2 --CRH CRHR2 --UCN2 CRHR2 --UCN3
# [5] UCN --CRHBP UCN --CRHR1 CRH --CRHR1 UCN2 --IL10RB
# [9] UCN3 --CRHR1 UCN3 --IL10RB IL10RB--IL22 IL10RB--IL28A
# [13] IL10RB--IL10 IL10RB--IL10RA IL10RB--IL28B IL22 --IL22RA2
# [17] IL22 --IL22RA1 IL28A --IL28RA IL28RA--IL29 IL10 --IL10RA
نلاحظ ان الحزمة اعطتنا بعض المعلومات عن الشبكة. الجملة IGRAPH UN-- 17 20 -- تخبرنا ان المخطط غير موجه UN وانه يحتوي على 17 عنصر تتفاعل فيما بينها عن طريق 20 ضلع.
لرسم شبكة التفاعل يمكننا استعمال دالة plot. تمكننا هذه الدالة من تحديد الكيفية التي نريد رسم المخطط كلون الرؤوس, حجمها, طريقة توزيع الرؤوس في المخطط (او الـ layout مثلا, على شكل دائرة او باستعمال خوازميات تنسيق ).
plot(G, layout=layout.lgl,
vertex.label.cex= 0.5,
vertex.color="#a1d99b",
edge.label.family="sans",
vertex.label.color = "black",
edge.color="black",
edge.curved=.1)
مثلا هذا المثال يعطينا الشكل التالي:
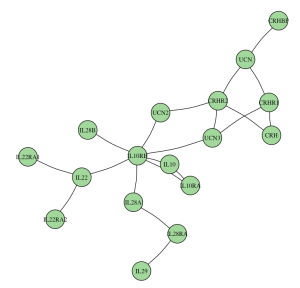
يمكننا ايضا انشاء الشبكات عن طريق استعمال مصفوفة المحاذات باستعمال دالة graph_from_adjacency_matrix. في العادة نستعمل هذه الطريقة لما نحسب الاضلع بطريقة اوتوماتيكية. مثلا انطلاقا من التعبير الجيني نقوم بحساب معامل الارتباط بين الجينات و نقوم وصل الجينات المترابطة عن طرق الاضلع.
في هذا المثال سوف ننشئ مصفوفة بطريقة عشوائية و نقوم يتحويلها الى شبكة.
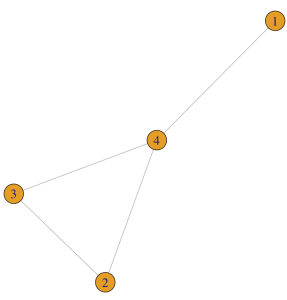
A <- matrix(sample(c(1,0),size = 16,replace = TRUE,prob = c(0.3,0.7)),ncol = 4,byrow = 4) # [,1] [,2] [,3] [,4] # [1,] 1 0 0 0 # [2,] 0 0 1 1 # [3,] 0 1 0 0 # [4,] 1 1 1 0 G2 <- graph_from_adjacency_matrix(A,mode="undirected",diag = FALSE) plot(G2)
مثلا هنا تحصلنا على هذا المخطط
الطريقة الثالثة التي يمكننا استعمالها لإنشاء المخططات هي استعمال عبارات من لغة مبسط مُعَرفة igraph من طرف يمكن من خلالها تحديد الطريقة االتي ترتبط بها الرؤوس. الدالة المسؤولة عن قراءة هذه العبارات وتحويلها الى شبكات هي دالة graph_from_literal. العبارات المستعملة تحتوي على معاملات خاصة بالأضلاع وأخرى بالرؤوس. حيث يرمز الى الرؤوس بالستعمال الحروف او الارقام. اما معاملات الأضلاع فهي تتكون من سلسلة من + و -. يرمز - الى ان الضلع غير موجه و الـ + الى اتجاه الضلع.
مثلا: A-B و A-----B تعطي مخطط غير موجه يربط بين الرأسين A و B. لتحديد اتجاه التوجيه يمكننا كتابة A-+B لتوجيه الضلع من A نحو B, او A+-Bلتوجيهه من B نحو A. يمكننا ايضا تجميع الرؤوس في مجموعات مثلاA:B -+ C:D تسمح لنا بربط A و B بكل من C و D. في المثال التالي نوضح بعض الحالات:
G3 <- graph_from_literal(A -- B) # IGRAPH UN-- 2 1 -- # + attr: name (v/c) # + edge (vertex names): # [1] A--B G4 <- graph_from_literal(A -+ B) # IGRAPH DN-- 2 1 -- # + attr: name (v/c) # + edge (vertex names): # [1] A->B G5 <- graph_from_literal( A -+ B:C) # IGRAPH DN-- 3 2 -- # + attr: name (v/c) # + edges (vertex names): # [1] A->B A->C G6 <- graph_from_literal( A -+ B:C, C-+ D -+A) # IGRAPH DN-- 4 4 -- # + attr: name (v/c) # + edges (vertex names): # [1] A->B A->C C->D D->A
حساب بعض خصائص الشبكات
بعد انشاء المخططات في العادة يكون اهتمامنا منصبا على استخراج بعض المعلومات من هذه العلاقة. مثلا ايجاد العناصر الرئيسية, العناصر اكثر ارتباطا, ... الخ من التحليلات التي تهم دراستنا. حزمة igraph توفر العديد من الدوال المفيدة لحساب المعايير. في المثال التالي نبين بعض الدوال التي يمكن استعمالها:
sort(degree(G)) # CRHBP IL28B IL22RA2 IL22RA1 IL29 CRH UCN2 IL28A IL10 IL10RA # 1 1 1 1 1 2 2 2 2 2 # IL28RA UCN UCN3 CRHR1 IL22 CRHR2 IL10RB # 2 3 3 3 3 4 7 sort(betweenness(G)) # CRHBP IL10 IL10RA IL28B IL22RA2 IL22RA1 IL29 # 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 0.0000000 # CRH CRHR1 UCN2 IL28RA UCN CRHR2 IL28A # 0.5833333 12.5000000 15.0000000 15.0000000 15.5833333 26.7500000 28.0000000 # IL22 UCN3 IL10RB # 29.0000000 35.8333333 92.7500000 sort(edge.betweenness(G)) # [1] 1.000000 6.416667 10.750000 11.250000 15.000000 15.000000 16.000000 16.000000 # [9] 16.000000 16.000000 16.000000 18.583333 19.916667 20.250000 23.333333 25.750000 # [17] 30.000000 42.000000 42.000000 45.750000 sort(closeness(G)) # IL29 CRHBP IL22RA2 IL22RA1 CRH IL28RA UCN # 0.01449275 0.01470588 0.01785714 0.01785714 0.01818182 0.01851852 0.01886792 # IL28B CRHR1 IL10 IL10RA CRHR2 IL22 IL28A # 0.02222222 0.02272727 0.02272727 0.02272727 0.02380952 0.02439024 0.02439024 # UCN2 UCN3 IL10RB # 0.02702703 0.02857143 0.03333333
يمكننا تلخيص هذه القيم في هذا الرسم حيث يمثل حجم الرأس قيمة المركزية. نلاحظ انه بالنسبة لهذا المخطط هناك تشبابه في بعض النتائج, لكن بعض الرؤوس المهمة في بعض المركزيات لم تكن مهمة في مركزية اخرى.

بالإضافة الى معايير المركزية, يمكننا ايضا القيام ببعض عمليات التجميع التي تسمح لنا باكتشاف المجموعات المترابطة في الشبكة. توفر حزمة igraph العديد من الخورزميات للقيام بذلك, لكن في هذا المثال سوف نستعمل خوارزمية cluster_fast_greedy. بعد تطبيق هذه الخوارزمية يمكننا الحصول على قائمة المجتمعات باستمعمال دالة groups. لإخبار الآر بأننا نريد رسم حيز حول كل مجموعة نقوم باعطاء قائمة المجموعات باستعمال خاصية mark.groups في دالة plot كما هو موضح في المثال التالي:
clus <- cluster_fast_greedy(G)
grp <- groups(clus)
plot(G,layout = layout.lgl,edge.arrow.size=.15,
#vertex.size=20,
vertex.color="#a1d99b",
vertex.frame.color= "#a1d99b",
vertex.label.color = "black",
vertex.label.cex= 0.8,
edge.label.color="#d62728",
edge.label.cex=1.5,
edge.label.family="sans",
edge.color="black",
vertex.label.family = "sans",
edge.curved=.1,
mark.groups = grp)
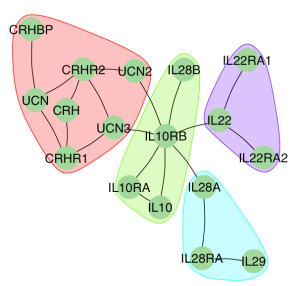
إضافة بعض الخصائص للرؤوس و الأضلاع
في بعض الاحيان نريد ان نضيف بعض المعلومات للرؤوس و الأضلاع, مثلا لون كل ضلع, خصائص البروتين, وزن الضلع ... الخ من الخصائص. يمكننا إضافة هذه الخصائص بأستعمال دلة V()E() لتغير خصائص الأضلع.
مثلا V(G)$color <- "red" تسمح بتغيير لون كل الرؤوس الى الاحمر. اما V(G)[[1]]$color <- "red" فتسمح فقط بتغير لون الرأس الاول. و E(G)$width = 2 تعطي الوزن 2 لكل الأضلاع. في المثال التالي سوف نقوم بتغيير حجم الرؤوس والاضلع استنادا الى المركزية الوسطية ونقوم بتلوين العنصر الرئيسي باللون الاحمر.
G8 <- G
V(G8)$color <- "#a1d99b"
V(G8)[["IL10RB"]]$color <- "red"
V(G8)$size <- 4 *log(betweenness(G8) + 1)
E(G8)$width <- 0.15 * edge.betweenness(G8)
plot(G8,layout = layout.lgl,edge.arrow.size=.15,
vertex.label.color = "black",
vertex.label.cex= 0.8,
edge.label.color="#d62728",
edge.label.cex=1.5,
edge.label.family="sans",
edge.color="gray80",
vertex.label.family = "sans",
edge.curved=.1)

خلاصة
في هذا المقال عرفنا ببعض مفاهيم الشبكات من الجانب الرياضي و قمنا باعطاء نظرة مختصرة عن كيفية التعامل مع الشبكات في لغة الآر باستعمال حزمة igraph. بطبيعة الحال ما تم تغطيته في هذا المقال يعتبر فقط مقدمة للمبتدئين في هذا المجال وفي لغة الآر خاصة. بالإضافة الى لغة الآر هناك العديد من اللغات التي تسمح للك بالتعامل مع الشبكات بالإضافة الى بعض البرامج كبرنامج Cytoscape و Gephi وغيرها. شخصيا ان افضل التعامل مع الشبكات باستعمال الآر خاصة في الحالات التي لاتوجد برامج تقوم بما اريد ثم اقوم بحفض المخطط على شكل GML باستعمال دالة write.graph ثم رؤيته باستعمال برامج مثل Gephi.
في الأخير اتمنى ان يكون هناك من استفاد من هذا المقال.
مصادر
- Dirk Koschützki and Falk Schreiber (2008). Centrality Analysis Methods for Biological Networks and Their Application to Gene Regulatory Networks. Gene Regul Syst Bio, 2: 193–201.
- Mahdieh Ghasemi et al (2014). Centrality Measures in Biological Networks. CURRENT BIOINFORMATICS.
- Gabor Csardi and Tamas Nepusz (2006). The igraph software package for complex network research. InterJournal Complex Systems,, 1695.
- Zhou et al (2014). Human symptoms–disease network . Nat Commun, 289-293.
رابط المقالة : المعلوماتية الحيوية بالعربية » التعامل مع الشبكات الحيوية برمجيا باستعمال لغة الآر