مدخل إلى الاحتمالات واختبار الفرضيات (الجزء الثاني)

(مصدر الصورة)

فيما سبق كان اهتمامنا بقيمة المتغير 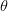$\theta$ (أو المَعْلَمة كما تسمى في بعض المصادر) لاستعمالها من أجل الاستدلال الاحصائي لكن في بعض الأحيان يكون لدينا فرضية حول قيمة المتغير ونريد أن نعرف مامدى صحة هذه الفرضية. مثلا, نريد التأكد من صحة الفرضية القائلة أن معدل طول الرجال أكبر من معدل طول النساء, أو مثلا التأكد من أن تعبير جين معين في الخلايا السرطانية أكبر من نسبة تعبيره في الخلايا العادية. في هذه الحالة يمكننا القيام باختبار احصائي يسمى إختبار الفرضيات.

رأينا في جزء التقدير النُقطي أن قيمة التقدير لديها نسبة من التباين, فلو فرضت أن المتوسط يساوي 0 ثم قدرته ووجدت أنه 0.5 هذا لا يعني أن قيمة المتغير الحقيقية مختلفة عن الصفر اختلافا جوهريا, لأن القيمة التي تم تقديرها كانت مبنية على العينة المأخوذة وليس كل المجتمع, لهذا يجب حساب قيمة احصائية تخبرك بمدى صحة فرضيتك وهو المبدا وراء إختبار الفرضيات.

رياضيا يمكننا أن نرى أن المسألة تتلخص في تحديد ما إذا كان المتغير 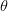$\theta$ ينتمي إلى مجموعة 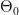$\Theta_0$ التي نفترضها أو المجموعة 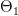$\Theta_1$ (في عادة النفي) . نسمي الفرضية القائلة بأن 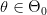$\theta \in \Theta_0$ بـ الفرضية الصفرية ( Null Hypothesis) أو فرضية العدم (مثلا لا يوجد علاقة بين الطول والجنس) ونرمز لها بالرمز 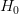$H_0$ ونسمي الفرضية الأخرى بـ الفرضية البديلة ونرمز لها بـ 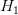$H_1$ . أو بصفة عامة نكتب:

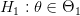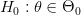
$H_1 : \theta \in \Theta_1$ ضد $H_0 : \theta \in \Theta_0$

يمكننا تلخيص بعض الحالات في هذا الجدول:

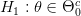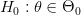
$H_1 : \theta \in \Theta_0^c$ ضد $H_0 : \theta \in \Theta_0$

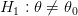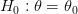
$H_1 : \theta \ne \theta_0$ ضد $H_0 : \theta = \theta_0$

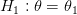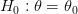
$H_1 : \theta = \theta_1$ ضد $H_0 : \theta = \theta_0$

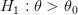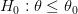
$H_1 : \theta > \theta_0$ ضد $H_0 : \theta \leq \theta_0$

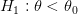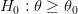
$H_1 : \theta < \theta_0$ ضد $H_0 : \theta \geq \theta_0$

في العادة نريد أن نثبت أن الفرضية الصفرية خاطئة. مثلا أفرض أن تعبير الجين متساوي في الخلية السرطانية و الخلايا السليمة وأحاول حساب قيمة حسابية تخبرني بمدى صدق الفرضية الصفرية, في العادة تسمى هذه القيمة p-value مثلا إذا كانت هذه القيمة تساوي 0.04 هذا يعني أنه لدي إمكانية 96% أن أقول أن تعبير الجين مختلف بين العينتين ونسبة الخطأ في هذا التصريح هي 4%.

لكن لا نستبق الأحداث الآن وسنصل إلى مفهوم الـ p-value فيما بعد.

طرق القيام بإختبار الفرضيات:

الآن بعدما كتبنا المشكلة بطريقة رياضية نريد أن تكون لدينا دالة رياضية تمكننا بالقيام بالاختبار. هناك عدة طرق يمكن استعمالها للقيام بذلك. في هذا المقال سوف نشرح الطريقتين الأكثر استعمالا وهما إختبار نيمان-بيرسن (Neyman-Peatson test) و إختبار تناسب دوال الإمكان ( Likelihood Ratio Test). بناءا على مبدا هذين الطريقتين يمكننا استنتاج معادلات طرق الإختبار المعروفة مثل إختبار تي (T-test) و الكاي تربيع (test-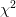 $\chi^2$ ), ... إلخ.

1) إختبار نيمان-بيرسن ( Neyman-Pearson Test):

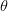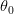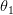يستعمل هذا النوع من الاختبار عند المقارنة بين قيمتين. مثلا لدينا اختبار وندري أن قيمة المتغير $\theta$ تكون إما $\theta_0$ أو $\theta_1$ . أو إختصارا:

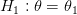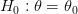
$H_1 : \theta = \theta_1$ ضد $H_0 : \theta = \theta_0$

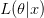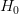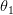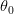إذا كانت دالة الإمكان للعينة هي $L(\theta|x)$ يمكن حساب منطقة رفض الفرضية الصفرية $H_0$ بالمجال الذي تكون فيه قيم دالة الإمكان أكبر عندما نعوض بقيمة المتغير $\theta_1$ و نعرف منطقة القبول بالمجال التدي تكون فيه دالة الامكان أكبر عندما نعوض بقيمة $\theta_0$ .

رياضيا يمكننا تعريف منطقة الرفض 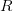$R$ بـ:

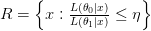
$R=\left\{ x: \frac{L(\theta_{0}|x)}{L(\theta_{1}|x)} \leq \eta\right\}$

ومنطقة القبول بـ:

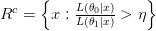
$R^c=\left\{ x: \frac{L(\theta_{0}|x)}{L(\theta_{1}|x)} > \eta\right\}$

إذا كانت الفرضية البديلة صحيحة فإنه في حالة استعمال 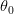$\theta_0$ سيكون إحتمال أن تكون البيانات في منطقة الرفض صغيرا إذْ أننا نتوقع أن تكون كل القيم قادمة من الدالة ذات المتغير 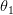$\theta_1$ . لهذا من أجل تحدد قيمة 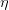$\eta$ بالقيمة التي تسمح لنا بقبول 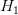$H_1$ بنسبة خطأ 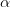$\alpha$ . أو بطريقة أسهل يمكننا كتابة:

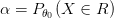
$\alpha = P_{\theta_0}(X \in R)$

في العادة نتقبل الفرضية البديلة بنسبة خطأ 1%, 5% أو حتى 10% في بعض التطبيقات الطبية.

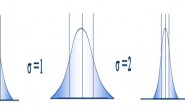
رسم توضيحي بين منطقة القبول

1) إختبار تناسب دوال الامكان (Likelihood Ration Test) :

يعتبر هذا الاختبار تعميما لاختبار نيمان-بيرسن, حيث أنه في هذه الحالة عوض المقارنة بين قيمتين للمتغير, يتم إختبار ما إذا كان المتغير 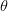$\theta$ ينتمى إلى مجال من القيم أو آخر. اختصارا يمكن كتابة:

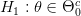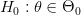
$H_1 : \theta \in \Theta_0^c$ ضد $H_0 : \theta \in \Theta_0$

في هذه الحالة يمكننا التفكير كالتالي: بما أن دالة الإمكان هي التي تخبرنا بمدى تفسير النموذج الاحصائي للبيانات, فيكفي أن أقارن أكبر قيمة للدالة في المجال 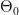$\Theta_0$ وأكبر قيمة للدالة في المجال 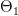$\Theta_1$ وبالتالي يصبح لدي إختبار مشابه لاختبار نيمان-بيرسن ونقوم بتحديد قيمة الخطأ ... إلخ.

يمكننا تعريف القيمة الاحصائية للاختبار (Test statistics) كالتالي:

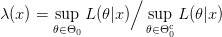
$\lambda(x) = \sup\limits_{\rm \theta \in \Theta_0} L(\theta | x) \Big / \sup\limits_{\rm \theta \in \Theta_0^c} L(\theta | x)$

وبعدها نعرف منطقة الرفض 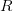$R$ بالمنطقة التي تكون فيها :

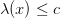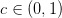
$\lambda(x) \leq c$ بحيث $c \in (0,1)$

لنفرض مثلا لوكان لدينا عينة مأخوذة من توزيع طبيعي 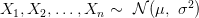$X_1,X_2, \dots, X_n \sim\ \mathcal{N}(\mu,\,\,\sigma^2)$ ولتسهيل الأمور لنفرض أننا نعرف قيمة 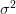$\sigma^2$ لكن لا نعرف قيمة 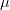$\mu$ ونريد أن نتأكد من الفرضية:

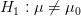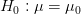
$H_1 : \mu \ne \mu_0$ ضد $H_0 : \mu = \mu_0$

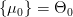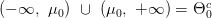نقوم أولا بتحديد المجالات في كل من الفرضيات. لدينا $\{ \mu_0 \} = \Theta_0$ و $(-\infty,\,\, \mu_0)\,\,\cup\,\,(\mu_0,\,\, +\infty) = \Theta_0^c$ .

ثم نحدد دالة الامكان :

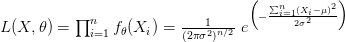
$L(X,\theta) = \prod_{i=1}^{n} f_\theta(X_i) = \tfrac{1}{(2\pi\sigma^2)^{n/2}}\; e^{\Big ( -\frac{\sum_{i=1}^{n}(X_i-\mu)^2}{2\sigma^2} \Big ) }$

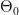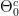ثم نقوم بحساب قيمة الامكان الأكبر في كلا المجالين $\Theta_0$ و $\Theta_0^c$ :

في المجال 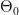$\Theta_0$ بما أنه توجد قيمة واحدة فأكبر قيمة 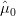$\hat\mu_0$ يمكن أتأخذها دالة الإمكان في هذا المجال هي فقط في القيمة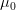 $\mu_0$

$\hat\mu_0 = \mu_0 = \underset{\mu \in \Theta_0}{\operatorname{argmax}} L(\theta | x)$

إذن:

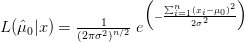
$L(\hat\mu_0 | x) = \tfrac{1}{(2\pi\sigma^2)^{n/2}}\; e^{\Big ( -\frac{\sum_{i=1}^{n}(x_i- \mu_0)^2}{2\sigma^2} \Big ) }$

في المجال 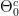$\Theta_0^c$ يمكننا حساب قيمة الإمكان الأكبر بحساب القيمة التي تجعل المشتقة تساوي صفر فنجد أنها تساوي قيمة الوسط الحسابي:

$\hat\mu_1 = \underset{\mu \in \Theta_0^c}{\operatorname{argmax}} L(\theta | x) = \tfrac{1}{n}\,\sum_{i=1}^n x_i = \bar x$

نعوض هذه القيمة في دالة الإمكان فنجد :

$L(\hat\mu_1 | x) = \tfrac{1}{(2\pi\sigma^2)^{n/2}}\; e^{\Big ( -\frac{\sum_{i=1}^{n}(x_i-\bar{x})^2}{2\sigma^2} \Big ) }$

يمكننا الآن حساب القيمة الإحصائية 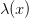$\lambda(x)$ وبعد بضع عمليات الاختزال نتحصل على:

$\lambda(x) = \tfrac{L(\mu_0 | x)}{ L(\bar{x} | x) } = exp \Big [ - \tfrac{(\bar{x}-\mu_0)^2}{2\sigma^2/n} \Big ]$

لدينا العبارة 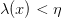$\lambda(x)< \eta$ مكافئة للعبارة:

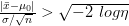
$\tfrac{| \bar{x}-\mu_0 |}{\sigma / \sqrt{n}} > \sqrt{-2\,\, log{\eta}}$

للتبسيط الكتابة نضع 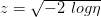$z = \sqrt{-2\,\, log{\eta}}$ . يمكننا إذن تعريف منطقة الرفض 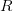$R$ كماهو في المعادلة وكما هو موضح في الشكل.

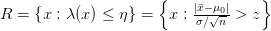
$R=\left\{ x: \lambda(x) \leq \eta\right\} = \left\{ x: \tfrac{|\bar{x}-\mu_0|}{\sigma / \sqrt{n}} > z \right\}$

إذا كانت لك خلفية عن اختبار الفرضيات فسترى أن هذا المجال شكله مألوف. في الحقيقة ماهو إلا إختبار زي للعينة الواحدة ثنائي الحد (two sided Z-test for one sample).

رسم بياني يوضح منطقة الرفض في إختبار زي للعينة الواحدة.

يمكننا إذن بنفس الطريقة تحديد أنواع الإختبارات للحالات الأخرى.

طرق تقييم اختبار الفرضيات:

كما نوهنا فيما سبق أنه بعد تحديد منطقة الرفض يجب تحديد مدى نسبة الخطأ الذي يمكننا ارتكابه عن رفض الفرضية الصفرية أو ما يسمى بالـ p-value. بالإضافة إلى قيم أخرى يمكننا تلخيصها في الجدول التالي:

توضيح القيم المستعملة لقيم إختبار الفرضيات

في هذا الجدول يمكننا أن نلاحظ أنه يمكننا القيام بأربعة أنواع من القرارت إثنان منها صحيحة (الأحمر و الأخضر الداكن) و إثنان منها خاطئة (الأخضر الفاتح و البنفسجي).

في الحالات الصحيحة هو عندما تكون لدينا قيم تنتمي إلى الفرضية الصفرية و نصنفها على أنها تنتمي للفرضية الصفرية (المربع الأخضر) أو عندما تكون تنتمي إلى الفرضية البديلة ونصنفها على أنها في الفرضية البديلة (المربع الأحمر).

لكن يمكننا أن نرتكب نوعين من الأخطاء:

- خطأ من النوع الأول (Type I error) : في هذه الحالة (المربع البنفسجي) تكون لدينا بيانات تنتنمي إلى الفرضية الصفرية لكن صنفناها على أنها في الفرضية البديلة وتسمى هذه القيمة بـ 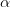$\alpha$ أو p-value.

مثلا لو قمنا باختبر تغير التعبير الجيني للجينات بين الخلايا السرطانية و الخلايا العادية ثم صنفنا مجموعة منهم أنها على أن تعبيرها تغير (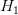 $H_1$ ) لكن في الحقيقة تعبيرها لم يتغير ( 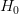$H_0$ ). في هذه الحالة نقوم مثلا بالاختبار بنسبة خطأ 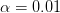$\alpha = 0.01$ لتقليل الأخطاء.

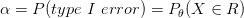
$\alpha = P(type\,\, I\,\, error) = P_\theta(X \in R)$

-خطأ من النوع الثاني (type II error) : هذا النوع من الخطأ ( المربع الأخضر الفاتح) يخبرنا بنسبة القيم التي نهتم بها لكن صنفت على أساس أنها غير مهمة. ويرمز عادة إلى هذا الخطأ بالرمز 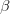$\beta$ .

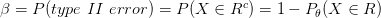
$\beta = P(type\,\,II\,\, error) = P(X \in R^c) = 1- P_\theta(X \in R)$

تقاس قوة الإختبار بمدى قدرته على رفضه الفرضية الصفرية لما تكون هذه الأخيرة خاطئة. مثلا نقول أن إختبارنا قوي إذا كانت رفضنا للجينات التي لا تظهر إختلافا جوهريا في تعبيرها بين الخلايا السرطانية و الخلايا العادية.

يمكننا كتابة معادلة قوة الإختبار كالتالي:

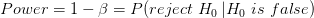
$Power = 1- \beta = P(reject\,\,H_0\, | H_0\,\, is \,\, false)$

خلاصة:

يمكننا تلخيص عملية القيام بعملية إختبار الفرضيات في الخطوات التالية:

1) كتابة معادلة الإمكان

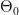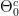2) تحديد المجالات $\Theta_0$ و $\Theta_0^c$ .

3) حساب قيمة الامكان الأكبر في المجال 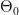$\Theta_0$ .

4) حساب قيمة الامكان الأكبر في المجال 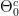$\Theta_0^c$ .

5) حساب معادلة القيمة الاحصائية للإختبار.

6) تحديد منطقة الرفض.

7) تقييم الإختبار

في الأخير أتمنى ان يفيد هذا المقال البعض و عذرا على التفصيل في بعض المعادلات الرياضية لكن من وجهة نظري أظن أن معرفة المبدأ وراء هذا النوع من الإختبار هو المهم لانه يسهل علينا فهم نتائج هذه الاختبارات لأننا في العادة لسنا مظطرين للقيام بهذه الحسابات لتوفرها في الكثير من لغات البرمجة. كما يمكن للقارئ أن يستخرج معادلة إختبار الفرضيات في حالة ما كانت لديه بيانات لها توزيع مغاير للتوزيعات المستعملة بكثرة.

ربما في المقالات القادمة سوف نتكلم عن بعض الاختبارات المعروفة مثل إختبار تي واختبار ويلكوكسن (Wilcoxon test) وغيرها. لكن هذا المقال فقط مدخل ولم نتكلم عن الكثير من الأشياء.

رابط المقالة : المعلوماتية الحيوية بالعربية » مدخل إلى الاحتمالات واختبار الفرضيات (الجزء الثاني)