بسم الله الرحمن الرحيم,
في المقالات السابقة نوهنا كثيرا إلى اختبار الفرضيات (Hypothesis Testing) وأهميته في تحليل البيانات, لهذا في هذا المقال نريد أن نوضح بعض مبادئ الاحتمالات الاساسية ثم الدخول في شرح الفكرة العامة وراء اختبار الفرضيات. المحتوى العربي في هذا المجال متوفر بكثرة على شكل مقلات أو حتى فيديوا لكن أريد ان أشرحها بطريقة متدرجة مع البرهنة على بعض المعادلات لجعل القارئ يفهم المبدء وراء المعادلات من أجل استعمال احسن لهذه الاختبارات, والهدف الثاني هو ربط هذه المعلومات مع مجال المعلوماتية الحيوية.
لهذا السبب تم تقسيم المقال إلى جزئين لأعطاء نظرة شاملة عن الطرق الموجودة
مدخل إلى الاحتمالات:
الهدف الاساسي لعلمتي الاحصاء و الاحتمالات هو استخراج معلومات من البيانات عن طريق صياغتها بطريقة رياضية تمكننا من تلخيص محتواها و التنبئ بالقيم المستقبيلة لهذه البيانات. فعلمُ الاحتمالات مثلا يسمح لنا بتقدير نسبة وقوع حادثة ما, مثلا ماهو احتمال سقوط الأمطار أو أحتمال الحصول على رقم 6 عند رمي حجرة النرد,... إلخ.
لحساب هذه الاحتمالات في العادة ناخذ مجموعة من العينات ونحاول ان نستنتج نسبة الحصول على بعض القيم في المجتمع. مايجب التنبه إليه هنا هو أننا نأخذ جزء (عينة) ونحاول وصف الكل (المجتمع) وهذا ما يسمى بالاستدلال الاحصائي (Statistical Inference). مثلا لنفرض أننا نريد دراسة نسبة الشباب (أقل من 30 سنة) في العالم العربي, الحل الأمثل هو أن آخذ سجلات الاحصاء السكاني في كل بلد عربي و أقوم بعَدْ اشخاص هذه الفئة. لكن المشكلة أن مواردي محدودة ولاستطيع الوصول إلى كل هذه السجلات. الحل الوحيد الذي يبقى في يدي هو أن استجوب عشوائيا عددا من الناس مثلا 1000 شخص من كل أقطار العالم العربي و استنادا إلى هذه النتائج يمكنني تقدير نسبة الشباب في العالم العربي. مثلا لو قابلة 700 شاب خلال هذا الاستجواب فسوف يتكون لدي تصور أن حوالي 70% من العالم العربي شباب.
مثال عن توزيع السكان في المجتمع السعودي (المصدر)
لورسمنا الجدول التكراري للتوزيع العمري للسكان للاحظنا أنه يمكننا محاكات شكل هذا التوزيع باستعمال معادلة رياضية  f_\theta(x)
f_\theta(x) مما يسهل علينا القيام ببعض الاستنتاجات دون اللجوء إلى البيانات. لاحظ الاحصائيون أن بعض التوزيعات تتكرر بشكل كثير في انواع عديدة من البيانات فقاموا باعطاء الصيغة العامة للدوال التي تمككنا من وصف هذه الأشكال. مثلا من بين هذه التوزيعات لدينا التوزيع الطبيعي (توزيع غوس, Gaussian distribution) للبيانات التي تكون أغلب قيمها مركزة حول نقطقة واحدة بطريقة متوازية , التوزيع الثنائي (Binomial distribution) للبيانات التي تتكون قيمتبين ... إلخ.
مما يسهل علينا القيام ببعض الاستنتاجات دون اللجوء إلى البيانات. لاحظ الاحصائيون أن بعض التوزيعات تتكرر بشكل كثير في انواع عديدة من البيانات فقاموا باعطاء الصيغة العامة للدوال التي تمككنا من وصف هذه الأشكال. مثلا من بين هذه التوزيعات لدينا التوزيع الطبيعي (توزيع غوس, Gaussian distribution) للبيانات التي تكون أغلب قيمها مركزة حول نقطقة واحدة بطريقة متوازية , التوزيع الثنائي (Binomial distribution) للبيانات التي تتكون قيمتبين ... إلخ.
رياضيا يمكننا أن نتخيل أن البيانات التي تحصلنا عليها أُخذت عشوائا من نموذج احصائي (دالة)  f_\theta(x)
f_\theta(x) بحيث أن
بحيث أن  \theta
\theta يمثل مجموعة المعاملات التي تحدد شكل الدالة. مثلا في التوزيع الطبيعي
يمثل مجموعة المعاملات التي تحدد شكل الدالة. مثلا في التوزيع الطبيعي 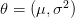 .
.
بصفة عامة يمكننا كتابة:
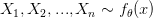 بحيث
بحيث 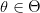
إذا فرضنا أن بياناتنا تتبع توزيعا ما, مثلا التوزيع الطبيعي, يجب علينا في الخطوة القادمة تحديد قيمة المعامل 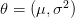 . لكن كيف يمكننا أختيار أحسن قيمة للمعامل
. لكن كيف يمكننا أختيار أحسن قيمة للمعامل 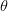 التي تسمح لنا بالمُحاكات الأمثل لتوزيع البيانات؟
التي تسمح لنا بالمُحاكات الأمثل لتوزيع البيانات؟
الامكان الأكبر و دالة الامكان :
يمكننا التعبير عن امكانية الحصول على القيم 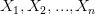 من الدالة
من الدالة 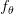 بالمعادلة :
بالمعادلة :
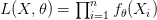
تسمى هذه الدالة بـ دالة الإمكان ( Likelihood function) حيث أنها تخبرنا بمدى امكانية الحصول على هذه القيم من الدالة 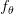 . يمكننا أن نستنتج إذا أنه كلما كانت هذه القيمة أكبر دلّ ذللك أن النموذج
. يمكننا أن نستنتج إذا أنه كلما كانت هذه القيمة أكبر دلّ ذللك أن النموذج 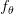 أقرب إلى تمثيل التوزيع الحقيقي للقيم. مثلا إذا كان لدينا توزيع طبيعي, يمكننا حساب احتمال الحصول على القيمة
أقرب إلى تمثيل التوزيع الحقيقي للقيم. مثلا إذا كان لدينا توزيع طبيعي, يمكننا حساب احتمال الحصول على القيمة 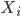 هو:
هو:
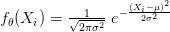
إذن دالة الامكان الأكبر تساوي:
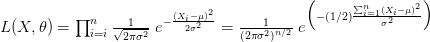
في هذه المعادلة قيم المتغير 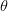 هي الوحيدة الغير معروفة. يعني لو أردنا الحصول على أكبر قيمة لدالة الامكان
هي الوحيدة الغير معروفة. يعني لو أردنا الحصول على أكبر قيمة لدالة الامكان 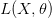 يجب علينا إيجاد قيمة
يجب علينا إيجاد قيمة 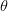 التي تعطينا أحسن محاكات للبيانات ولتكن
التي تعطينا أحسن محاكات للبيانات ولتكن  . تسمى قيمة
. تسمى قيمة  بـ الإمكان الأكبر (Maximum likelihood) .
بـ الإمكان الأكبر (Maximum likelihood) .
بصفة عامة إذا كان 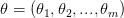 يمكننا حساب قيمة
يمكننا حساب قيمة 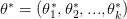 بحساب القيم التي تجعل المشتقة الأولى لدالة الإمكان تساوي الصفر و المشتقة الثانية سالبة.
بحساب القيم التي تجعل المشتقة الأولى لدالة الإمكان تساوي الصفر و المشتقة الثانية سالبة.
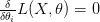 و
و 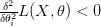
أو بصيغة أخرى:

مثلا في حالة التوزيع الطبيعي يمكن حساب قيمة الامكان الأكبر 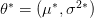 كالتالي (للتفاصيل يمكن الإطلاع هنا ):
كالتالي (للتفاصيل يمكن الإطلاع هنا ):
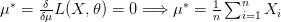
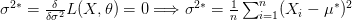
بما أننا نعلم أن للتوزريع الطبيعي قمة واحدة يمكننا عدم حساب المشتقة الثانية.
نلاحظ من هذا المثال أنه في حالة التوزيع الطبيعي, المتوسط الحسابي والتباين تمثلان أحسن تقدير للحصول على أكبر قيمة لدالة الإمكان.
تسمى العملية التي قمنا بها سابقا (حساب قيمة  ) في علم الاحصاء بالتقدير النقطي (Point estimation) حيث أن اهتمامنا في هذه الحالة كان ايجاد أحس تقدير للتوزيع البيانات. قيمة
) في علم الاحصاء بالتقدير النقطي (Point estimation) حيث أن اهتمامنا في هذه الحالة كان ايجاد أحس تقدير للتوزيع البيانات. قيمة  التي تحصلنا عليها في هاذه الحالة تمثل نتجية تجربة واحدة فلو أعدنا التجربة مرة أخرى و أخذنا قيما عشوائية من
التي تحصلنا عليها في هاذه الحالة تمثل نتجية تجربة واحدة فلو أعدنا التجربة مرة أخرى و أخذنا قيما عشوائية من 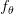 سوف نتحصل على قيم
سوف نتحصل على قيم 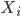 أخرى وبالتالي قيمة مختلفة لـ
أخرى وبالتالي قيمة مختلفة لـ  . يعني أننا لو أعدنا التجربة عدة مرات سوف نتحصل على قيم كثيرة لـ
. يعني أننا لو أعدنا التجربة عدة مرات سوف نتحصل على قيم كثيرة لـ  ولنرمز لها بـ
ولنرمز لها بـ 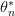 .
.
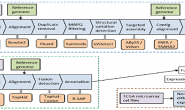
لهذا السبب هناك عدة نقاط يجب الانتباه إليها عند القيام بالتقدير النقطي , لكي لا نطيل المقال يمكننا تلخيصها في الجدول التالي حيث أن 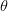 ترمز للتقدير الحقيقي:
ترمز للتقدير الحقيقي:
|
التوافق( Consistency ) |
|
|
عدم الانحياز ( Unbiasedness ) |
|
|
أصغر قيمة تباين (Minimum variance) |
هي الأصغر بالنسبة للتقديرات الأخرى |
|
أصغر قيمة خطأ تربيعي (Minimum mean square error) |
هي الأصغربالنسبة للتقديرات الأخرى |
ي هذا المقال تنوقف عند هذا القدر لكي لا يكون مملا ونكمل جزء اختبار الفرضيات في الجزء القادم. الهدف من هذا المقال هو تعريف القارئ بالمدئ وراء دالة الامكان الأكبر والتي لها دور مهم في فهم المبدأ وراء إختبار الفرضيات, لأن الهدف هنا ليس اعطاء معادلات للحفظ لكن لاعطاء القارئ نوعا من الحدس وراء هذا المبدأ أما بالنسبة للمعادلات فهي متوفرة في مواقع عدة. أتمنى أن يكون المقال مفيدا خاصة للجدد في المجال.
رابط المقالة : المعلوماتية الحيوية بالعربية » مدخل إلى الاحتمالات واختبار الفرضيات (الجزء الأول)


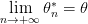
![E[\theta_n^*]= \theta](http://www.bioinfo4arabs.com/wp-content/plugins/latex/cache/tex_8a1548d20943b3ae338c48327bed9512.gif)
![Var[\theta_n^*]](http://www.bioinfo4arabs.com/wp-content/plugins/latex/cache/tex_470c607c1e503a9486322dcea7d20789.gif)